Chapter1 RStudio and R Basics

R is a language and programming environment for statistical computing and graphics, which offers an ‘Open Source’ (freely available) alternative for implementation of the S language, which is the usual language of choice when it comes to statistical computing. In other words, R is a freely available software environment which runs on Windows, MacOS and LINUX, that allows the user to conduct mathematical calculations, data manipulation, statistical computations and create graphical output.

RStudio is known as an integrated development environment (IDE) for R, which essentially provides more user friendly access to R and its features. The figures below show the two environments separately. The first is the original R environment and the second is RStudio. Even from these simple graphics you can see that RStudio provides a much more detailed user face, with a number of different ‘panels’ (discussed in more details later) for a range of different commands.

Figure 1.1: R Environment.

Figure 1.2: RStudio IDE.

1.1 How to install R and RStudio

Installing R and RStudio requires two separate steps:

Firstly, we need to install the original R software for your specific operating system (Windows, Mac or LINUX) from https://cran.ma.imperial.ac.uk/. Once this is installed, you are able to open R and you should be met with a screen similar to Figure:1.1, above. At this point, you are now able to use R and all its features completely. However, as mentioned in the previous section, it is usually preferable to work with RStudio due to its user friendly interface.
To download the free version of RStudio, visit https://rstudio.com/products/rstudio/download/ and download ‘RStudio Desktop (Free)’. Once downloaded, you will be able to open RStudio and should see a similar screen to that of Figure:1.2. Keep in mind that the image(s) above may be running older versions than the one you are now using. Once you have downloaded RStudio, I recommend you only ever use R through this platform, so there is no need to open the original R software.

Note: In order to use R through the RStudio environment, you MUST first download the original R software.

If you are using a university computer, you do not have to worry about the steps above as R and RStudio are already installed and can be found within the list of installed programmes.

1.2 RStudio interface explained

When you open RStudio, you will notice that the environment has a number of different ‘panels’. You may find that your environment looks slightly different to the one in the figure above and may only have one larger panel on the left hand side rather than two separate ones. This difference will be explained later. To avoid confusion, in the first instance your screen should look like the figure given below:

Figure 1.3: Orginal RStudio View.

Let us discuss each of the panels and some of their associated tabs, in a little more detail:

Console (Left panel) - The console is the panel you will interact with the most, as this is where you can type commands which can be ‘Run’ to produce output.
Environment (Top right panel, Tab 1) - The environment tab lists all active objects that have been ‘assigned’ (see below) and stored for later use. This is especially helpful when writing a longer programme with a large number of variables needing to be stored, as it allows you to refer back to previously defined objects.
History (Top right panel, Tab 2) - The history tab shows a list of all commands that have been run within the console so far. Again, this can prove useful when writing long programmes which may require re-use of certain commands or to double check what has already been run.
Files (Bottom right panel, Tab 1) - The file tab shows the folder of your ‘Working Directory’. That is, the folder in which R is directed to look for data sets etc. This tab looks similar to the equivalent folder in your PC/Mac folder window.
Plots (Bottom right panel, Tab 2) - The plots tab allows you to view all of the graphs/plots you have created within that session. This proves helpful when you want to compare a variety of plots.
Packages (Bottom right panel, Tab 3) - The packages tab provides access to a list of ‘Packages’ or ‘Add-ons’ needed to run certain functions. When RStudio first starts, it will only have access to its basic packages which contain fundamental functions and tools. In order to conduct more sophisticated analysis or calculations it is usually required for you to install extra packages which contains these tools.
Help (Bottom right panel, Tab 4) - The help tab can be used to find additional information about certain functions, tools or commands within RStudio. You will find this to be a very important part of your programming experience and will be used constantly. We will discuss later on how to access help via a shortcut through the console.

1.3 Mathematical calculations

Now that we understand a little more about the setup of R and RStudio, we want to discuss what we can actually do in R. As previously mentioned, R is most notably used to conduct mathematical calculations, data manipulation, statistical computations and create graphical output but let us discuss each of these in a little more detail and give some practical examples you can try for yourself.

In its most basic form, R can be used as a large scale calculator. In contrast to an actual calculator, it can perform a variety of calculations quickly and easily, which would otherwise take a great deal of time, e.g. series summations and matrix multiplication. In fact, there are many calculations that can be performed in R which would not be possible even with a scientific calculator.

1.3.1 Basic numerical calculations

If you simply type 5*3 into the ‘console’ (see above) and press enter you should receive the solution as an output which again appears in the console below your input:

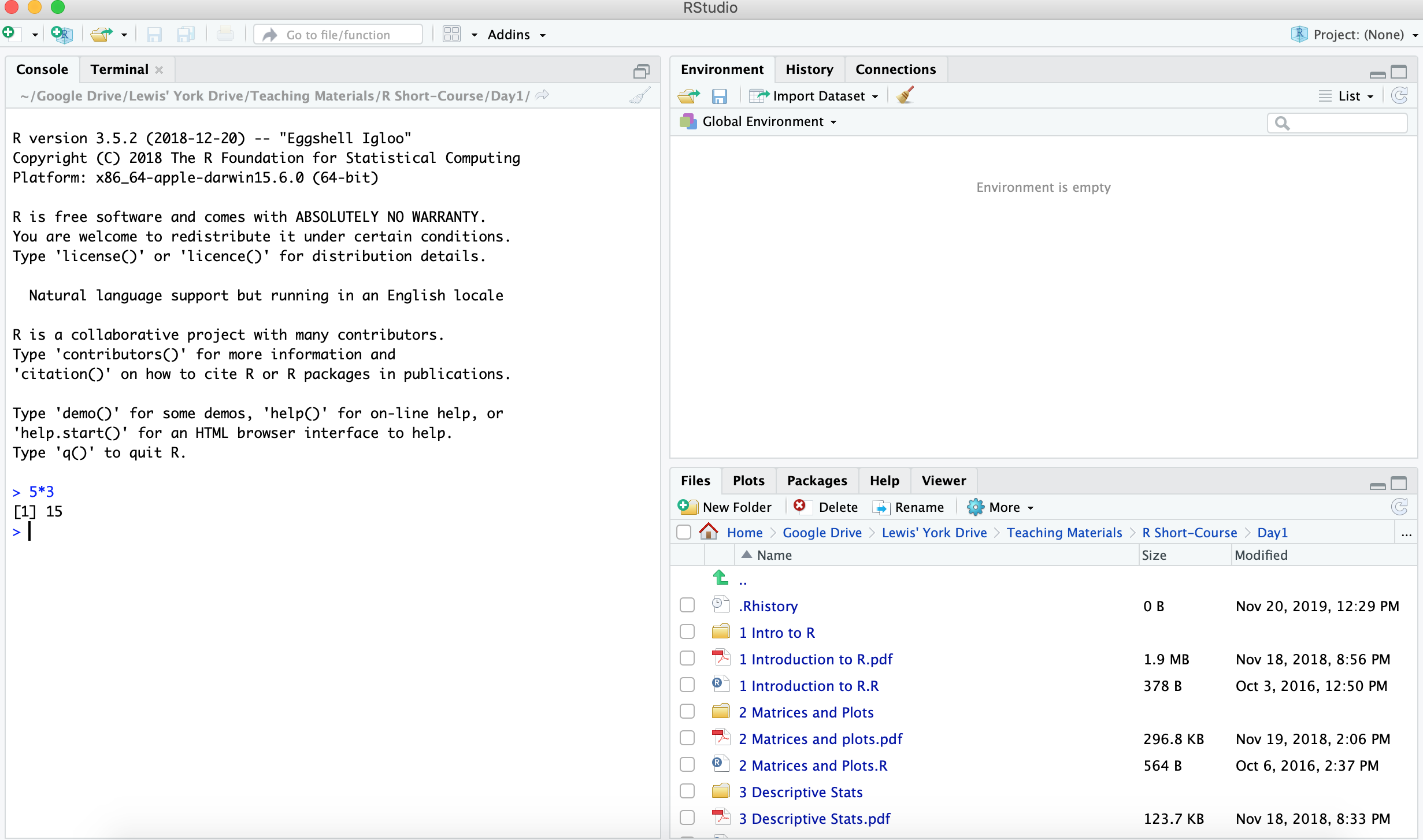
Figure 1.4: Basic Multiplication.

In a similar way, you can perform a variety of other basic mathematical calculations:

7+3

## [1] 10

9/3

## [1] 3

15-2

## [1] 13

6^3

## [1] 216

sqrt(100)

## [1] 10

Notice that some calculations, like the square root above, require knowledge of certain ‘functions’ e.g. sqrt() of which there exists hundreds in R’s base packages for you to use. Knowing what each of them are and how they work is part of the programming experience and will take time. We will talk more about ‘functions’, and how you can create your own in a later chapter.

Some other useful examples of pre-defined variables and functions you are likely to use are pi, exp() and log() which allow use of \(\pi\), \(e^x\), \(\ln(x)\) in calculations, respectively. For example, if we wanted to calculate \(e^{\ln(\pi)}\):

exp(log(pi))

## [1] 3.141593

1.3.2 More complicated calculations

Imagine that you want to find the sum of all the integers from \(1\) to \(1000\). To do this on a basic calculator would require you to physically type each integer in turn, adding them as you go along (assuming you do not know the series summation formula). However, in R, you can compute this with one simple function, i.e. sum() with argument 1:1000, which creates the sequence of numbers from \(1\) to \(1000\). To see this in action before performing this particular calculation, type 1:10 in the console and press enter:

1:10

##  [1]  1  2  3  4  5  6  7  8  9 10

As you can see, the output is the required sequence of integers from \(1\) to \(10\). Returning to our original summation calculation, by inputting sum(1:1000) and pressing enter, R will first create the sequence from \(1\) to \(1000\) in a similar wat to above, then sum all of these values:

sum(1:1000)

## [1] 500500

Before we move on to discuss any further calculations, let us take a moment to highlight the disadvantages of writing code directly in the console itself and introduce something known as an ‘R script’. In addition, we will also discuss how we can ‘assign’ values to variables which we can then recall for calculations later on.

1.4 R script

So far, we have executed each line of code directly into the console itself, one line at a time, pressing enter and producing output each time. Although this works and produces the necessary output, it has numerous disadvantages. Firstly, if you make a mistake in the line of code, you cannot simply amend it. Instead, you have to ‘re-type’ the code again (there is actually a quicker method) on a new line without the mistake. Secondly, it requires you to execute every line of code once you have completed it. If you are writing a complex programme with many lines, this will become very frustrating especially if something goes wrong half way through and you have to re-write the entire code again. Finally, you cannot easily save your written code within the console to be re-opened and edited at a later date. In order to avoid all of these problems, from now on we will type all of our code into an ‘R script’, from which we can execute the code into the console.

To open an R script, click the icon which looks like a blank piece of paper with the small green plus sign in the top left hand corner of your screen, then click R Script:

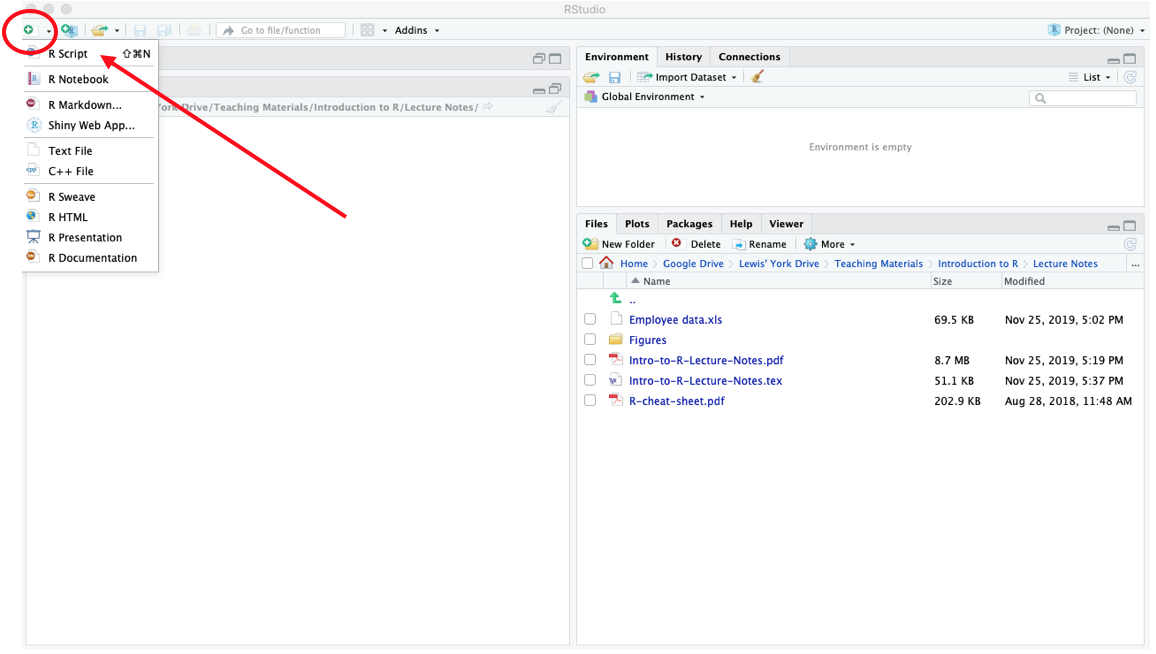
Figure 1.5: Opening an R script.

At this point, a new (blank) panel should open in the top left of your screen. This panel will now become the panel which you type all of your code (you no longer type into the console panel). Once you have typed your line of code, you can execute it (run it into the console) by simply highlighting the relevant code then clicking on the Run button as seen in Figure:@ref{fig:Script2} below.

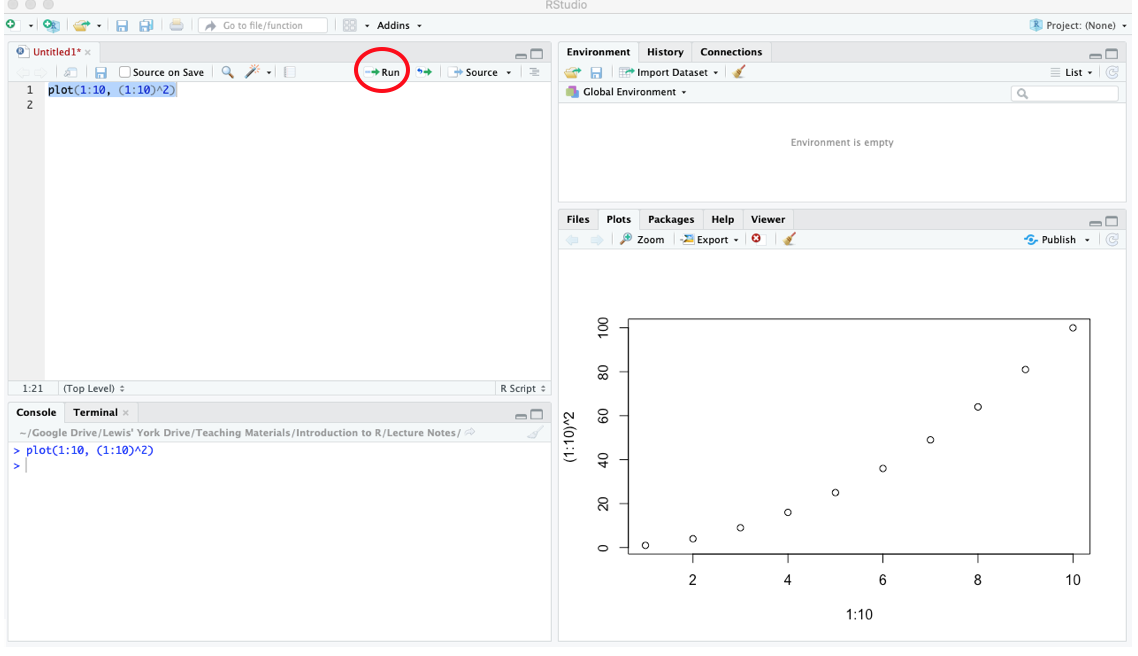
Figure 1.6: Executing code from a script in R.

Note you can also simply go to the start or end of the line and press Run, you do not actually need to highlight it. This is only necessary if you want to Run more than one line at a time.

By executing code from the script, you avoid all the previously discussed problems. That is, if you have a made a mistake in your code, which you will notice once executed, you now simply amend this in the script and re-run it which is much simpler than re-writing the entire code. Moreover, you do not actually have to execute any code until you desire. Think of the script as a notebook which you can keep typing in and can run code from whenever you wish. Finally, and most importantly, you can save the script file and re-open this at a later date to continue working on and/or send to a colleague. You do this in the normal way as if saving a standard document .

1.5 Assigning variables

Recall the earlier example where we calculated the sum of values from \(1\) to \(1000\). Although relatively straight forward, typing this code out each time we would like to use the result becomes tedious and is, in fact, unnecessary in R. Instead, R allows us to ‘assign’ a value, vector, matrix, function etc., to a variable so we can recall that particular quantity at any point by simply typing the variable itself. For example, instead of repeatedly typing sum(1:1000) or the result itself, we could ‘assign’ this to the variable \(x\) using the ‘assignment operator’ <-, which allows us to reuse the value later on by simply typing \(x\):

x <- sum(1:1000)
x

## [1] 500500

Note, however, that when we used the assignment operator it did not print the output itself, which would have happened if we had simply ran the code without assignment. This is the reason we then typed the variable \(x\) in the next line of the console, as this will now print as output whatever quantity is saved to the variable \(x\), in this case the sum of values from \(1\) to \(1000\). If you would actually like to do both things at the same time, i.e, assign and print the output, you should put the assignment code in brackets:

(x <- sum(1:1000))

## [1] 500500

## [1] 500500

Finally, when a variable is assigned, the variable name and the type of quantity that has been assigned to it, will be stored in the ‘environment’ tab/panel (top-right). In this case, the variable \(x\) was assigned and the quantity assigned to them takes the form of a ‘numeric’ (num) value.

1.6 Vectors

As we have already briefly seen within the summation calculations above, R can easily create collections of values in a single object, known as a vector, which can then be used in a variety of calculations, including vector and/or matrix type calculations themselves. There are in fact a number of different ways to create ‘vectors’ of values in R, so let us discuss some of the most common:

The most general way is to use the ‘combine’ or ‘concatenate’ function c(). This function combines a series of individual values and then glues them together to form a vector:

c(1, 2, 5, 9, 15)

## [1]  1  2  5  9 15

c(-3, 3, -1, 0, 10, 5, 2, -100, 25)

## [1]   -3    3   -1    0   10    5    2 -100   25

Although this is the most general method, it does require you to type out each value individually, not ideal if you want a vector containing \(1000+\) values.

We have already seen another example of how to create a vector using the colon syntax 1:1000. However, this is quite specific and only works for creating vectors which form a series of increasing/decreasing values with unit differences:

1:10

##  [1]  1  2  3  4  5  6  7  8  9 10

20:5

##  [1] 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5

2.5:10

## [1] 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5

The more general version of this method is to create a ‘sequence’ of values with an initial starting point, an end value and specifying the increments between the values:

seq(from=5, to=50, by = 5)

##  [1]  5 10 15 20 25 30 35 40 45 50

The third way requires a little more thought and experience but will become second nature once you get going. It involves using the previous method(s), as well as understanding how R deals with vectors in calculations, which you can then take advantage of (see below).

1.6.1 Vector calculations

Using vectors in calculations is just as simple as with scalar values, but will not necessarily produce the output you might first expect in some cases. Let us start by looking at some simple addition and subtraction:

a <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
b <- 11:20
a+b

##  [1] 12 14 16 18 20 22 24 26 28 30

b-a

##  [1] 10 10 10 10 10 10 10 10 10 10

Notice that the calculations in the above have been done ‘element-wise’ as you might expect. However, this is actually how R treats all standard vector-based calculations. This is a very important observation as it is a characteristic of R vector calculations that will come in handy throughout your coding life and should be utilised as much as possible. Let us look at a few more examples:

a*b

##  [1]  11  24  39  56  75  96 119 144 171 200

b/a

##  [1] 11.000000  6.000000  4.333333  3.500000  3.000000  2.666667  2.428571
##  [8]  2.250000  2.111111  2.000000

a^2

##  [1]   1   4   9  16  25  36  49  64  81 100

a^b

##  [1] 1.000000e+00 4.096000e+03 1.594323e+06 2.684355e+08 3.051758e+10
##  [6] 2.821110e+12 2.326305e+14 1.801440e+16 1.350852e+18 1.000000e+20

Once again, these have all been calculated element-wise! What happens if the vectors are not of the same length? In this case, R will automatically loop around the shorter vector and start using the values again from the beggining until it has used enough to match the length of the second vector. Let us take a look at a quick example to see how this works in practice:

vec1 <- c(1,2,3,4)
vec2 <- c(1,2,3,4,5,6,7)
length(vec1) # This function is used to print the number of elements within a vector.

## [1] 4

length(vec2)

## [1] 7

vec1 + vec2

## Warning in vec1 + vec2: longer object length is not a multiple of shorter
## object length

## [1]  2  4  6  8  6  8 10

This is a perfect example of why you need to be very careful when writing code. Just because you have (possibly) made a mistake, R will not always realise and execute a calculation anyway.

1.6.2 Vector strings

R is not all about numerical values. As a primary tool for statistical analysis, data can come in many shapes and sizes including words (known in R as character strings) or logical values, i.e, TRUE or FALSE. We will talk more about the latter values later but it is worth discussing ‘strings’ here.

A ‘character string’ is simply a word or combination of letters that you would like R to understand as such. To create or include a string, you need to use quotation marks:

"Hello World"

## [1] "Hello World"

Once you put quotation marks around something, R automatically recognises this as a string and will not try to perform any type of operation to this. This is even possible with numerical values:

"10 is a numerical value"

## [1] "10 is a numerical value"

As a small example, try adding together the strings “10” and “11” in R. Notice that because we have defined the values as strings, R cannot perform addition with them:

str("10")

##  chr "10"

str(10)

##  num 10

In exactly the same way as we have seen above, it is actually possible to create vectors of strings. This is very helpful when you want to name a bunch of objects, rows/columns in data tables or when they represent data points themselves, e.g., geographical regions etc.

c("York", "London", "Liverpool", "Birmingham")

## [1] "York"       "London"     "Liverpool"  "Birmingham"

1.7 Plotting graphs

One of R’s major strengths is the ease with which well-designed, publication-quality plots can be produced and can include mathematical symbols and formulae where needed. The basic plotting function in R, located in its basic packages, is the so-called plot() function. In its simplest form, the plot() function allows you to plot two variables, say \(X\) and \(Y\), against each other as a scatter plot. For example, imagine we wanted to plot the following points \((x,y)\): \[\begin{equation*} (0,0), \,(1,2),\, (2,2),\, (3, 5),\, (4, 4),\, (6, 8). \end{equation*}\] We could do this as follows:

X <- c(0,1,2,3,4,6)
Y <- c(0,2,2,5,4,8)
plot(X, Y)

From the plot above, you can see that R has simply taken the two vectors (X and Y) and plotted the values pairwise (as required) to create a basic scatter plot. That being said, the plot itself looks very basic and is not particularly aesthetic. This is because we have used the very basic structure for the plot() function. However, with a little alteration, this can be adapted to create something a little more exciting:

Figure 1.7: Example of Plot using plot().

The example above provides a small insight into the very basics of the plotting tools available in R. Let us look at this function a little more closely and is a perfect time to introduce R’s “query command”.

You can use the query command ? before a function or object to retrieve R’s information document associated to it. This document will appear in the bottom right panel and gives a break down of the functions purpose, format, variables and, in most cases, so examples of it in use.

Using ?plot() we find that the plot() function has the general form:

plot(x, y, main = , xlab = , ylab= , type= , pch= , col= , cex= , bty = )

where each of the arguments are defined as follows:

x - Points to be plotted along the x-axis
y - Corresponding points to plotted against the y-axis. Note that these values match-up pair-wise with the x values to create co-ordinate pairs \((x,y)\)
main - Takes a character string and gives the plot a main title
xlab - Takes a character string and labels the x-axis
ylab - Takes a character string and labels the y-axis
type - Takes a number of different character strings to define the type of plot desired, i.e. line, point etc. (see table below)
pch - Takes a values and defines the shape each point should take, i.e. circle, square etc. (see table below)
col - Sets the colours of the points/lines in the plot
cex - Takes a value and defines the size of the points
bty - Takes a character string and sets the type of axes for the plot

A number of other arguments can be used to change the layout and format of the plot but will not be discussed here. If you are interested, search for the par() function in the ‘Help’ tab or use ?par().

Example 1.1 Consider the followings prices on the equity index S&P500 for the last weeks:

day <- c(1:10)
price <- c(1979,1987,1951,1923,1920,1884,1881,1931,1932,1938)

Using a combination of all the arguments in the above list, we can produce the following plots:

plot(day, price)

plot(day, price,
     main="S&P 500",
     xlab="Day",
     ylab="Closing Price",
     pch=19,
     col=3,
     type="p")

plot(day, price,
     main="S&P 500",
     xlab="Day",
     ylab="Closing Price (£)",
     pch="+",
     col=2,
     type="b",
     bty="L")

The table below gives a non-exhaustive list of some of the different options you can make when choosing arguments for your plots. To find more, search online:

`type`	Description
“p”	points
“l”	lines
“b”	both
“c”	lines part alone of “b”
“h”	histogram like vertical lines
“s”	stair steps

`pch`	Description
0	square
1	circle
2	triangle
4	plus
5	cross
6	diamond

`bty`	Description
“o”	full box
“n”	no axes
“7”	top and right axes
“L”	bottom and left axes
“C”	top, bottom and right axes
“U”	bottom, left and right axes

1.7.1 Adding to plots (lines, points etc.)

There will be occasions where you wish to add another set of points, lines or plots to your original. This is usually the case when comparing two different sets of data or, for example, when wanting to draw a regression line through your data points. R has a variety of pre-defined functions that allow you to do this with ease. However, those who are new to R will make the common mistake of trying to add a second plot to the original by using the plot() function for a second time. The plot() function (seen above) does not simply plot points or lines. The source code underpinning the plot() function first instructs R to create a separate window/panel, create a set of axes (designed based on the choice of bty as argument) create some axis labels then, finally, add the points or lines. Therefore, by executing the function again, you will find you produce a completely new plot rather than adding to the previous.

In order to add more graphics to the original plot, we instead have to use the functions points(), lines() and abline(). The points() and lines() functions work in a very similar to that of the plot() function in the sense that they take similar arguments. The only difference now, is that the function does not first create axes etc., but will simply plot the points/lines onto the most recent plot that was created. Note here that since the points() function can take type as an argument, it is actually possible to create line plots with this function (type = "l") instead of using the abline() function. Remember, there are many ways to create the same output in R, it is down to you to decide which you prefer to use. Let’s add to the S&P 500 example above, by also adding the FTSE 100 prices during the same time period:

plot(day, price,
     main="S&P 500",
     xlab="Day",
     ylab="Closing Price (£)",
     pch="+",
     col=2,
     type="b",
     bty="L")
ftse <- c(1960, 1960, 1950, 1931, 1918, 1890, 1900, 1910, 1905, 1935)
points(day, ftse,
       col = "blue",
       type="b",
       pch="+")

The abline() function, on the other hand, is slightly different. This function is used simply to create straight lines on your current plot. Using ?abline() we see it takes the form

abline(a, b, h= , v = , ... )

The arguments in this case are no longer data points like in the previous plotting functions but correspond to co-ordinates:

a - The value of the intercept for the straight line
b - The value for the gradient of the straight line
h - The y co-ordinate (intercept) for a horizontal line
v - The x co-ordinate for the vertical line.

In addition to these arguments, you can also format the line type, width etc., but we will not discuss these again as they are simply aesthetic parameters which you can easily search for online.

plot(1:10, (1:10)^2,
     main="Abline example",
     ylab="y",
     xlab="x",
     type="b",
     pch=19,)

plot(1:10, (1:10)^2,
     main="Abline example",
     ylab="y",
     xlab="x",
     type="b",
     pch=19,)
abline(a=0,b=3, col = "red")
abline(a=0, b=6, col = "blue")
abline(h=60, lty = 2)
abline(v=6, lty = 3, lwd = 2, col = "orange")

In addition to the plot function and its variety of options, we can implement other plotting functions such as hist() and boxplot(), which will be discussed in a later chapter in more details, to produce the best graphical representation of your data possible. Finally, although we discuss graphics using the basic plotting commands here, it is worth pointing out the popularity of a completely different package and set of functions, known as ggplot2, which makes the plotting experience even more exciting. We will not actually discuss this in these lecture notes, however, it is strongly advised that you familiarise yourself with this package and its associated functions (for example using DataCamp). In fact, there are three excellent courses devoted to the subject which will be linked at the end of these notes.

1.8 Exercises

Exercise 1.1 Use R to compute the following quantities directly in the console:

\(\frac{7^3+ 5}{\sqrt{49}}\)
\(ln(100) - ln(10)\)
\(e^{ln(25)}\)
\(\pi^2\)
\(log_{10}(1000)\)

Exercise 1.2 Complete the following steps to familiarise yourself with working from an R script:

Open a new R Script
Write code that:

Computes the sum of the numbers from 1 to 500
Computes the square root of this sum

Run the script line-by-line
Save the script with a meaningful title.

Exercise 1.3 Create two vectors containing the numbers (5, 6, 7, 8) and (2, 3, 4), using c(). Assign these vectors to the variables u and v, respectively, and, unsing R, determine the following values:

The number of elements in each vector
\(u + v\)
\(u - v\)
\(u*v\)
\(\frac{u}{v}\)
\(u^v\)

Check the Environment tab and note what has been added.

Exercise 1.4 Create the vector of values \((1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5)\) using the following two methods:

Using the seq() function
Using only the colon syntax : and vectorised (element-wise) calculations.

Exercise 1.5 Create a vector containing all the square numbers from 1 up to and including 10,000 (\(100^2\)).

Exercise 1.6 The vectors LETTERS and letters are already pre-built into R’s base-package and contain the capital and lower-case versions of the letters from the English alphabet (Try it by simply running either LETTERS or letters in the console).

Create a vector containing the first 10 letters of the English alphabet in Capitals.
Now, using your solution from the previous part, create a new vector of the form: \[\begin{equation*} (A, A, A, B, B, B, C, C, C, \ldots, J, J, J). \end{equation*}\] [Hint: Try looking into the rep() function and how it works]

Exercise 1.7 Consider the following formula to calculate the number of mortgage payment terms required to pay off a mortgage as a function of the principle amount (\(P\)), the monthly repayments (\(M\)) and the monthly interest (\(i\)): \[\begin{equation*} n = \frac{\ln\left(\frac{i}{\frac{M}{P}-i}+1 \right)}{\ln(1+i)} \end{equation*}\]

Using R, solve the following problems:

Calculate the number of payments \(n\) for a mortgage with principle balance of £200,000, monthly interest rate of \(0.5\%\) and monthly payments of £2000.
Now construct a vector, named \(n\), of length 6 with the results of this calculation (in years) for a series of monthly payment amounts: \((2000, 1800, 1600, 1200, 1000)\).
Does the last value of \(n\) surprise you? Can you explain it?
Create a line plot for the values of \(n\) (excluding the last) against the different payment amounts. Give the plot a title, appropriate label names and make the points appear in blue.

1.9 Applied exercises

Exercise 1.8 A lender is analysing the behaviour of a simple loan under different interest rates and repayment assumptions.

Suppose a loan has an initial principal of £10,000 and accrues monthly compound interest. The balance after \(t\) months is given by:

\[ B_t = P(1+i)^t, \]

where

\(P\) is the initial principal
\(i\) is the monthly interest rate
\(t\) is the number of months

Assign the initial loan principal \(P=10000\) to a variable in R
Create a vector called months containing the values \(0, 1, 2, \ldots, 24\)
Suppose the monthly interest rate is \(0.4%\). Assign this value to a variable called i
Using vectorised calculations, compute the load balance over time and store the results in a vector called balance
Create a line plot of loan balance against time (months). Your plot should include:

A title
Axis lables
Blue points connected by lines

Now suppose the interest rate incrases to \(0.7%\) per month. Without changing the months vector:

Compute the new balances
Add this second balance path to the original plot, suing different colours and line type.

Briefly comment on how small chnages in the interest rate affect loan balances over time.